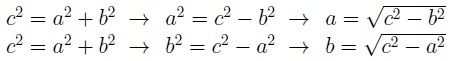El Teorema de Pitágoras
Pitágoras estudió los triángulos rectángulos, y las relaciones entre los catetos y la hipotenusa antes de probar su teoría.

El Teorema de Pitágoras
Si a y b son las longitudes de los catetos de un triángulo rectángulo y c es la longitud de la hipotenusa, entonces la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa.
Esta relación está representada por la fórmula:
|
Parece simple, pero intentemos con un triángulo rectángulo para ver si es cierto.

El teorema es válido para este triángulo — la suma de los cuadrados de los catetos es la misma cantidad que el cuadrado de la hipotenusa. Y, de hecho, es válido para todos los triángulos rectángulos (aunque, como puedes ver, no todas las medidas son número enteros como 3, 4, y 5).
Nota que el Teorema de Pitágoras no puede ser usado con cualquier triángulo — sólo aplica a los triángulos rectángulos.
Encontrando la Longitud de la Hipotenusa
Podemos usar el Teorema de Pitágoras para encontrar la longitud de la hipotenusa de un triángulo rectángulo si conocemos la longitud de sus catetos. Es decir, si conocemos las longitudes de a y b, podemos encontrar c.
Hagámoslo.

En el triángulo de arriba, nos dan las medidas de los catetos a y b: 5 y 12, respectivamente. Podemos usar el Teorema de Pitágoras para encontrar el valor de la longitud de c, la hipotenusa.
Ejemplo
| |||
Problema
|
Encontrar c cuando a = 5 y b =12
| ||
Teorema de Pitágoras
| |||
Sustituir a y b por los valores conocidos
| |||
Simplificar
| |||
Combinar términos semejantes
| |||
Calcular la raíz cuadrada en ambos lados
| |||
Solución
| |||
Usando la fórmula, encontramos que la longitud e de c, la hipotenusa, debe ser 13. (Aunque existen dos valores posibles de c que satisfacen la ecuación, 13 y -13, las longitudes son siempre positivas, por lo que podemos ignorar el valor negativo.)
¿Para cuál de los siguientes triángulos es
A)
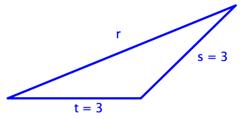
B)
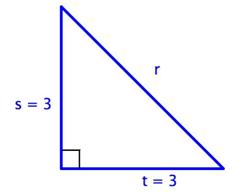
C)
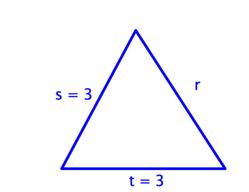
D)
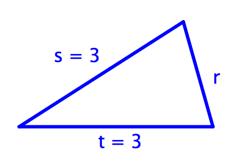 |
Encontrando la Longitud de un Cateto
Podemos también usar el Teorema de Pitágoras para encontrar la longitud de uno de los catetos de un triángulo rectángulo si nos dan las medidas de la hipotenusa y del otro cateto. Considera el triángulo siguiente:

Para encontrar la longitud del cateto a, podemos sustituir los valores b y c en la fórmula y luego usar un poco de razonamiento algebraico para calcular a.
Ejemplo
| |||
Problema
|
Encontrar a cuando b = 6 y c = 7
| ||
Teorema de Pitágoras
| |||
Sustituir b y c por los valores conocidos
| |||
Simplificar
| |||
Despejar el término a
| |||
Calcular la raíz cuadrada en ambos lados
| |||
Solución
|
A ≈ 3.61
| ||
Usando el Teorema de Pitágoras para Resolver Problemas Cotidianos
El Teorema de Pitágoras es una de las fórmulas matemáticas más útiles porque hay muchas circunstancias en el mundo real donde se puede aplicar. Por ejemplo, los arquitectos e ingenieros usan extensivamente esta fórmula cuando construyen rampas:
Los propietarios de una casa quieren convertir a una rampa los escalones que llevan del suelo al porche. El porche está a 3 pies sobre el suelo, y debido a regulaciones de construcción, la rampa debe empezar a 12 pies de distancia con respecto al porche. ¿Qué tan larga debe ser la rampa?
Para resolver un problema como este, normalmente dibujamos un diagrama simple que muestre los catetos y la hipotenusa del triángulo.
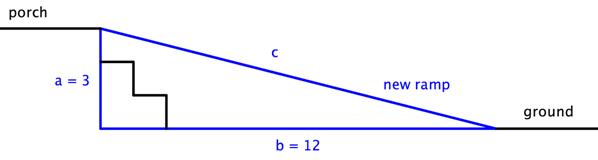
Observando el diagrama, podemos identificar los catetos y la hipotenusa del triángulo en el problema, Sabemos que el triángulo es un triángulo rectángulo porque el suelo y la parte del porche son perpendiculares, — esto significa que podemos usar el Teorema de Pitágoras para resolver este problema. Nos dan las longitudes de los catetos a y b, por lo que podemos usar esa información para encontrar la longitud de c, la hipotenusa.
Ejemplo
| |||
Problema
|
Encontrar c cuando a = 3 y b =12
| ||
Teorema de Pitágoras
| |||
Sustituir a y b por valores conocidos
| |||
Simplificar
| |||
Combinar términos semejantes
| |||
Calcular la raíz cuadrada en ambos lados
| |||
Solución
|
12.37 ≈ c
| ||
La rampa medirá alrededor de 12.37 pies.
Sumario
El Teorema de Pitágoras nos dice que para cualquier triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, El teorema está representado por la fórmula 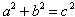 . Si conocemos las longitudes de dos de los lados del triángulo, podemos aplicar el Teorema de Pitágoras para encontrar la longitud del tercer lado.
. Si conocemos las longitudes de dos de los lados del triángulo, podemos aplicar el Teorema de Pitágoras para encontrar la longitud del tercer lado.